路径规划算法
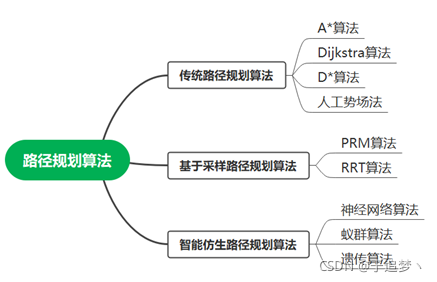
一、传统路径规划算法
1.Dijkstra算法
Dijkstra算法是Edsger Wybe Dijkstra在1956年提出的一种用来寻找图形中结点之间最短路径的算法。Dijkstra算法的基本思想是贪心思想,主要特点是以起始点为中心向外层层扩展,直到扩展到目标点为止。Dijkstra算法在扩展的过程中,都是取出未访问结点中距离该点距离最小的结点,然后利用该结点去更新其他结点的距离值。
Dijkstra算法流程:
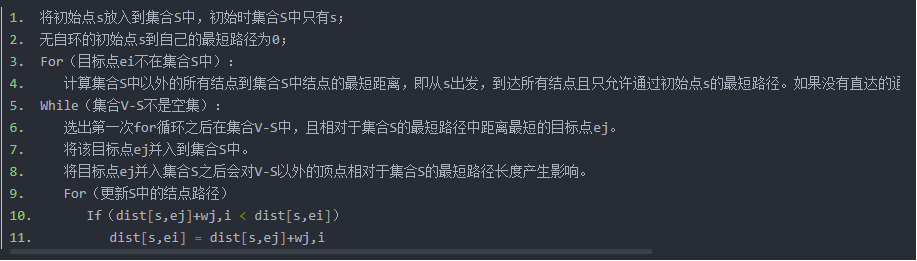
注:该算法不允许图中存在负权边。

优点:
1) 如果最优路径存在,那么一定能找到最优路径
缺点:
1) 有权图中可能是负边
2) 扩展的结点很多,效率低
2.A*算法
A算法发表于1968年,A算法是将Dijkstra算法与广度优先搜索算法(BFS)二者结合而成,通过借助启发式函数的作用,能够使该算法能够更快的找到最优路径。A算法是静态路网中求解最短路径最有效的直接搜索方法。
A算法的启发式函数:f(n)=g(n)+h(n)
f(n)表示结点的综合优先级,在选择结点时考虑该结点的综合优先级;
g(n)表示起始点到当前结点的代价值;
h(n)表示当前结点到目标点的代价估计值,启发式函数。
当h(n)趋近于0时,此时算法退化为Dijkstra算法,路径一定能找到,但速度比较慢;当g(n)趋近于0时,算法退化为BFS算法,不能保证一定找到路径,但速度特别快。我们可以通过调节h(n)的大小来调整算法的精度与速度。
在A*算法中,采用最多的是欧几里得距离,即dist = srqt((y2-y1)2+(x2-x1)2)。
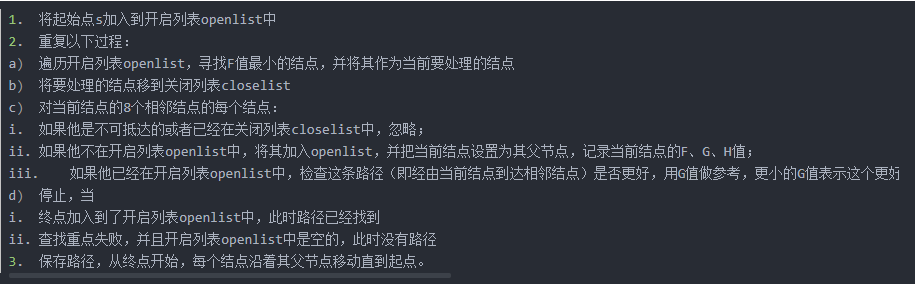
A*算法流程:

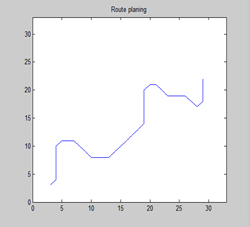
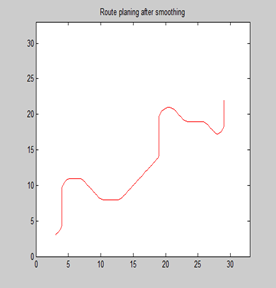
优点:
1) 利用启发式函数,搜索范围小,提高了搜索效率
2) 如果最优路径存在,那么一定能找到最优路径
缺点:
1) A算法不适用于动态环境
2) A算法不太适合于高维空间,计算量大
3) 目标点不可达时会造成大量性能消耗
3.D*算法
D算法是卡耐基梅隆机器人中心的Stentz在1994年提出的主要用于机器人探路,并且美国火星探测器上就是应用的D路径规划算法。A算法适用于在静态路网中寻路,在环境变化后,往往需要replan,由于A不能有效利用上次计算的信息,故计算效率较低。D算法由于储存了空间中每个点到终点的最短路径信息,故在重规划时效率大大提升。A是正向搜索,而D特点是反向搜索,即从目标点开始搜索过程。在初次遍历时候,与Dijkstra算法一致,它将每个节点的信息都保存下来。
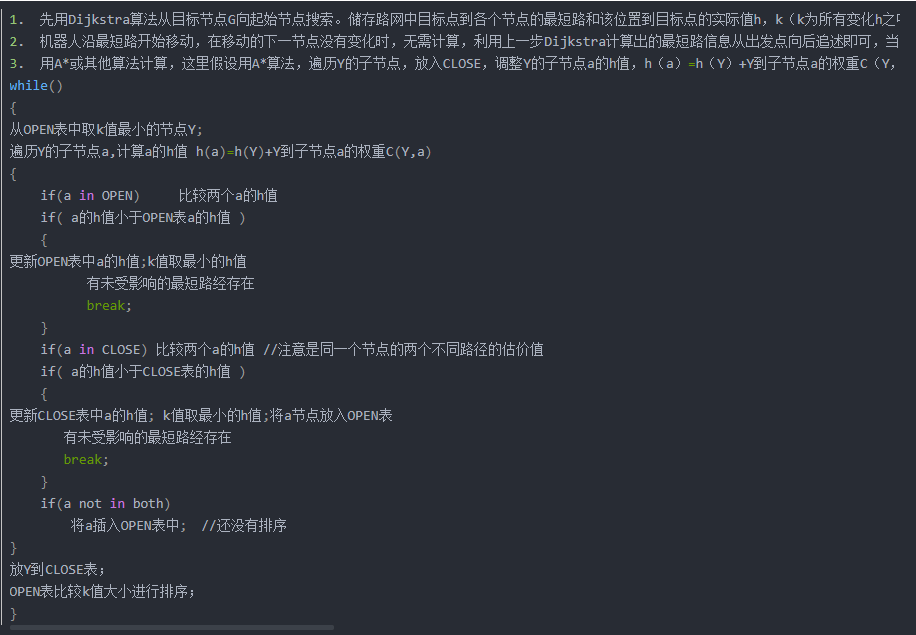
D*算法流程:
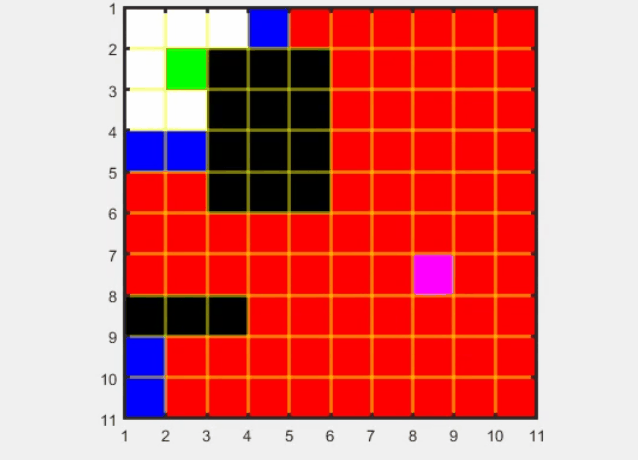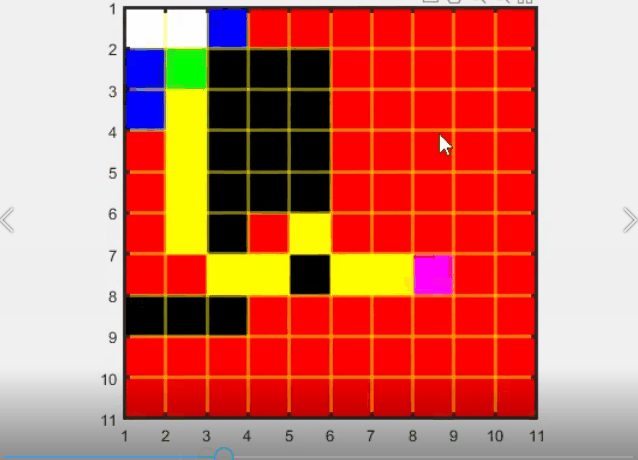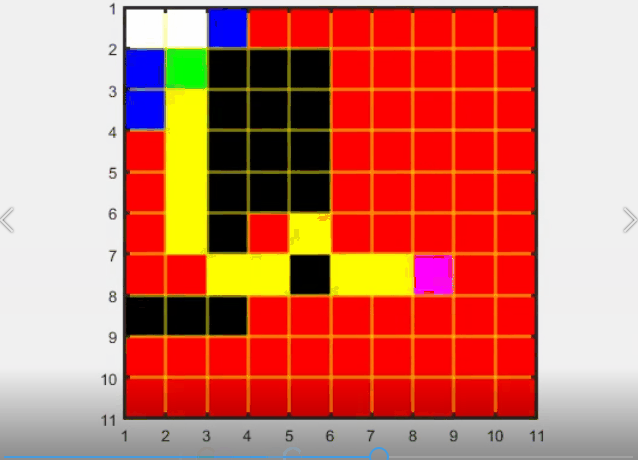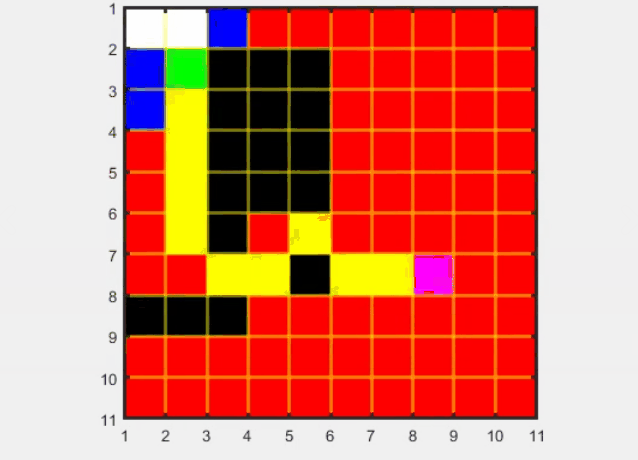
优点:
1)适用于动态环境的路径规划,搜索效率高
缺点:
1) 不适用于高维空间,计算量大
2) 不太适用于在距离较远的最短路径上发生变化的场景
4.人工势场法
人工势场法是由Khatib在1985年提出的一种基于虚拟力场的局部路径规划算法,该算法的基本思想是当机器人在周围环境中运动时,将环境设计成一种抽象的人造引力场,目标点对移动机器人产生“引力”,障碍物对移动机器人产生“斥力”,最后通过二者的合力来控制移动机器人的运动。应用人工势场法规划出来的路径一般是比较平滑并且安全的,但是存在着局部最优的问题。
利用势场函数U来建立人工势场,势场函数是一种可微函数,空间中某点处势场函数值的大小,代表了该点的势场强度。我们采用引力势场函数与斥力势场函数,用U(q)表示二者之和。
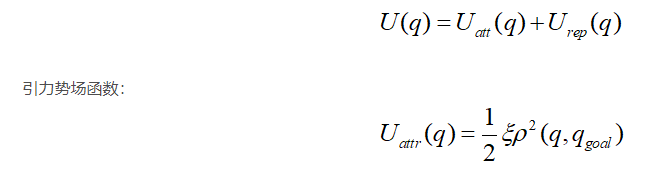
e表示引力增益,p(q,qgoal)表示当前点到目标点的距离;
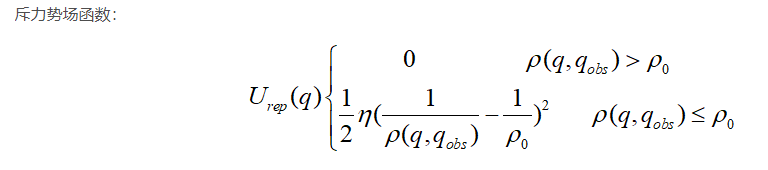
n表示斥力增益,p(q,qgoal)表示当前点到障碍物的距离,p0表示障碍物作用距离阈值。

优点:
1) 规划出的路径一般是比较平滑且安全
2) 人工势场法是一种反馈控制策略,具有一定的鲁棒性
缺点:
1) 容易陷入局部最优的问题
2) 距离目标点较远时,引力特别大,斥力相对较小,可能会发生碰撞
3) 当目标点附近有障碍物时,斥力非常大,引力较小,很难到达目标点
二、基于采样路径规划算法
1.PRM算法
随机路线图(PRM)算法是一种基于图搜索的算法,可以将连续状态空间转换成离散状态空间,在利用A*等搜索算法在路线图上寻找路径,提高搜索效率。PRM算法是概率完备且不是最优的算法。
PRM算法流程:


优点:
1) 适用于高维空间和复杂约束的路径规划问题
2) 搜索效率高,搜索速度快
缺点:
1)概率完备但不是最优
2.RRT算法
RRT算法是适用于高维空间,通过对状态空间中的采样点进行碰撞检测,避免了对空间的建模,较好的处理带有非完整约束的路径规划问题,有效的解决了高维空间和复杂约束的路径规划问题。该算法是概率完备但不是最优的算法。
RRT算法以初始点qinit作为根节点,通过随机采样增加叶子节点的方式,生成一个随机扩展树,当目标点位于随机扩展树上时,能够找到一天初始点到目标点的路径。首先,需要从状态空间中随机选择一个采样点qrand,然后从随机树中选择一个距离qrand最近的结点qnearest,从qnearest向qrand扩展一个步长的距离,得到一个新的结点qnew,如果qnew与障碍物发生碰撞,则返回空;否则,将qnew加入到随机树中,重复上述步骤直到qnearest和qgoal距离小于一个阈值。
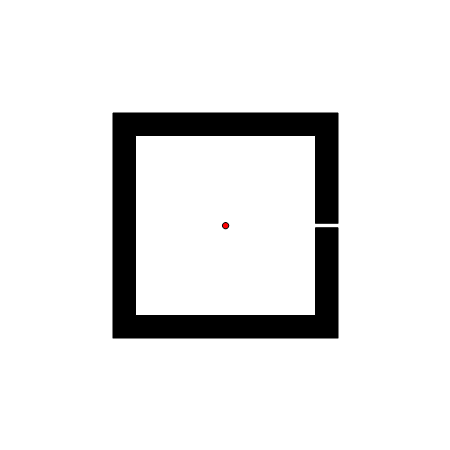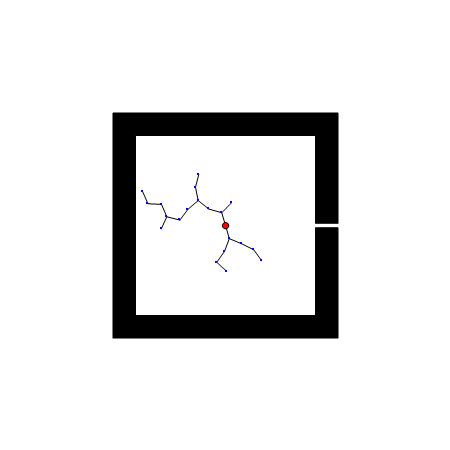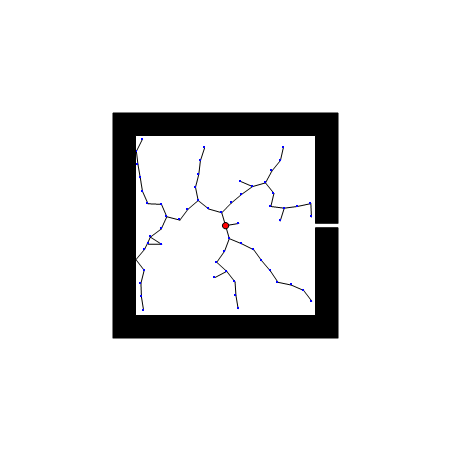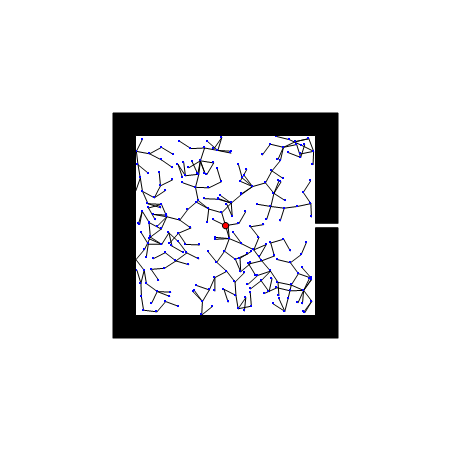
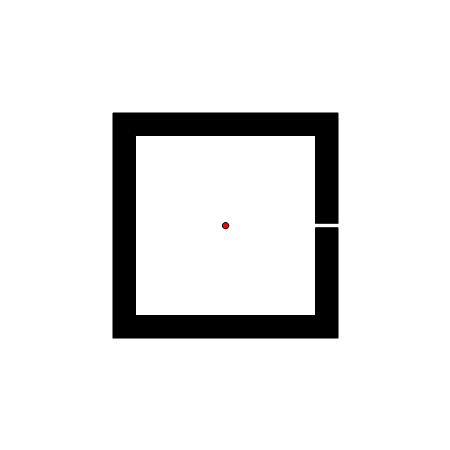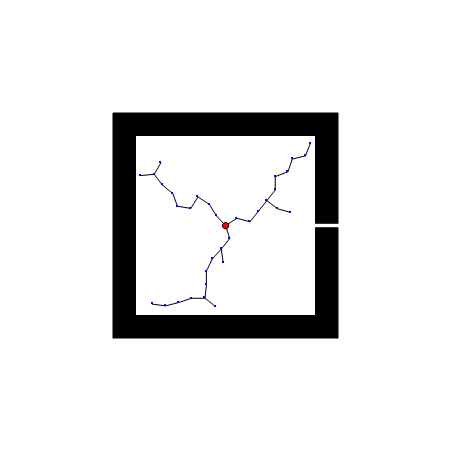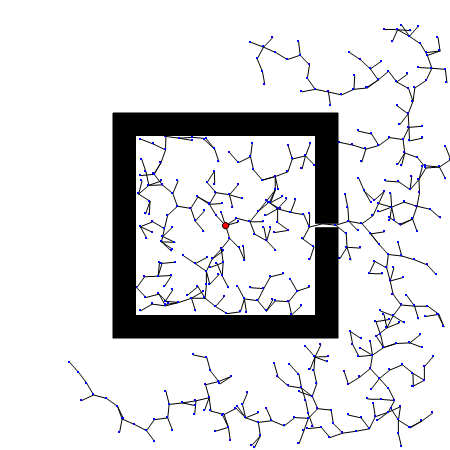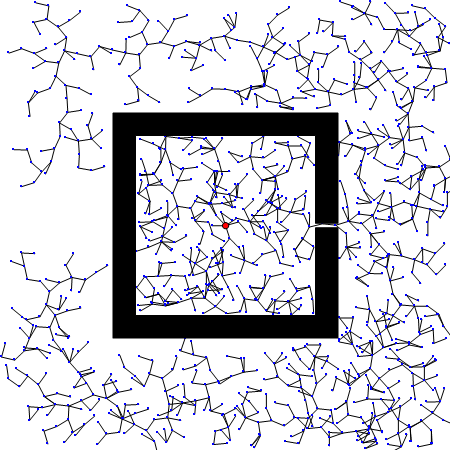
优点:
1) 搜索效率比较高,搜索速度比较快
2) 适用于高维空间,不会产生维度灾难的问题
3) 只需对状态空间采样点进行碰撞检测,避免了对空间的建模
缺点:
1) 规划出的路径质量一般,可能存在棱角、不够光滑
2) RRT算法不太适用于存在狭长空间的环境
3) 规划出的路径可能不是最优路径
4) 不适用于动态环境的路径规划
三、智能仿生算法
1.神经网络算法
随着机器人自主性的不断提高,使其具有环境感知以及环境学习的能力,许多学者提出了深度强化学习算法来解决移动机器人处于动态复杂环境中路径规划的问题。深度强化学习算法充分利用了深度学习的感知能力与强化学习的决策能力,通过机器人与环境的交互过程不断试错,通过环境评价性的反馈,实现系统更加智能的决策控制,帮助移动机器人在某些复杂未知的环境中实现一定程度的自主化与智能化。
路径规划就是一个标准的MDP问题,强化学习可以通过值迭代等方法建立一个表格,用以存储状态s到动作a的映射。但是在复杂环境中会产生维度灾难的问题,因此神经网络可以解决维度灾难的问题。以DQN算法为例,来讲解神经网络算法在路径规划中的应用。DQN算法是Q-Learning算法与卷积神经网络(CNN)二者进行结合。DQN算法是由两个网络结构、初始参数相同的结构组成,一个是估计网络,用来输出估计值函数;另一个是目标网络,用来输出目标值函数。通过强化学习使机器人与环境进行交互得到样本(s,a,r,s’),将所有的样本集放入到经验回放池中。神经网络进行训练时,随机的从经验回放池中抽取batchsz数量的样本,将样本输入进神经网络,利用神经网络的非线性拟合能力,拟合出非线性函数来表达我们的Q值,利用e-greedy策略来进行选择智能体的动作。智能体执行完相应的动作之后,环境会反馈一个状态和奖励值,最后经过神经网络模型的训练和优化得到网络的训练参数,得到相对准确的动作输出。
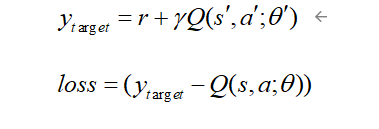
其中w表示估计网络的参数, w-表示目标网络的参数。
优点:
1) 适合于动态复杂环境
2) 适用于高维空间,避免维度灾难的问题
缺点:
1) 对硬件的要求比较高
2) 参数调节比较困难
2.蚁群算法
蚁群算法(Ant Colony Optimization,ACO)是Dorigo在1992年提出的一种用来寻找优化路径的概率型算法,是由一群无智能或有轻微智能的个体通过相互写作而表现出智能行为,为求解复杂问题提供了一个新的可能性。该算法的主要思想是蚂蚁在寻找食物过程中发现路径的行为。该算法具有分布计算、信息正反馈和启发式搜索的特征,本质上是进化算法中的一种启发式全局优化算法。
蚁群算法的基本原理是利用蚂蚁在觅食过程中会释放信息素。

影响蚁群算法的因素:
1) 信息素如何撒播
2) 信息素如何挥发
3) 以何种方式让蚂蚁选择运动方向,减少盲目性和不必要性
4) 给予蚂蚁和环境一定的记忆能力能够帮助减少搜索空间
个体分布越均匀,种群多样性就越好,得到全局最优解的概率就越大,但是寻优时间就越长;个体分布越集中,种群多样性就越差,不利于发挥算法的探索能力。正反馈加快了蚁群算法的收敛速度,却使算法较早地集中于部分候选解,因此正反馈降低了种群的多样性,也不利于提高算法的全局寻优能力。
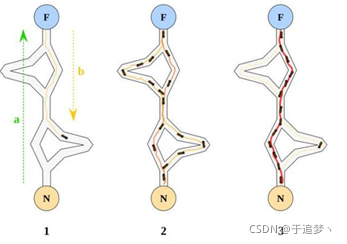
优点:
1) 蚁群算法的鲁棒性强
2) 采用正反馈机制,能够逼近最优解
3) 易与其他算法进行结合
缺点:
1) 盲目的随机搜索,搜索时间较长,搜索速度慢
2) 蚁群算法容易陷入局部最优
3) 蚁群算法参数的选择依赖于经验或试错
3.遗传算法
遗传算法(Genetic Algorithm,GA)是由John Holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的,来模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。其本质是一种高效、并行、全局搜索的方法,能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最佳解。

优点:
1) 遗传算法具有广泛的应用领域
2) 遗传算法具有群体搜索的特性
3) 遗传算法基于概率规则,搜索更为灵活
4) 遗传算法直接以目标函数作为搜索信息,不涉及目标函数值求微分的过程
缺点:
1) 遗传算法效率比较低
2) 遗传算法容易过早收敛
3) 遗传算法在编码时容易出现不规范不准确的问题
————————————————
原文链接:https://blog.csdn.net/qq_45875106/article/details/121314604
免责声明:CSDN博主「于追梦丶」的原创文章,文章版权归原作者于追梦所有,文中观点仅供分享交流,不代表本公众号立场。如涉及版权等问题,请您告知,我们将及时处理。