相较于传统的齿轮传动系统，目前高速化、集成化的电驱动系统新出现NVH问题的重点、难点主要有以下三点：转速逐步提高的高速驱动电机的影响；电机扭矩波动、径向力与齿轮传递误差等多个激励源的影响；考虑系统整体耦合变形的动力学响应分析建模。目前电驱系统减速器高速轴齿传动性能仿真技术正在处于发展阶段，国内外主机厂大部分处于起步阶段，减速器轴齿性能仿真模型精度不高、系统集成度不高、效率低、计算分析结果不够准确。考虑驱动电机结构、齿轮-传动轴-轴承的转子系统以及差速器壳体、电驱动系统箱体等异形部件，搭建电驱动系统刚柔耦合动力学模型，并给出了考虑驱动电机径向力、扭矩波动以及齿轮传递误差等振动激励源作用下的电驱动系统动力学响应的分析方法。

在传统内燃机汽车中，发动机噪声较好地掩盖了齿轮传动系统的振动噪声，但在纯电动汽车中，由于发动机噪声掩蔽效应的缺失，使得电磁噪声及齿轮阶次噪声凸现。此外，高速化、集成化发展给电驱动系统的NVH带来了新的挑战。目前电驱动系统的高速驱动电机的转速普遍高达12 000 r/min～18 000 r/min，预计在未来会进一步提高至20 000 r/min～25 000 r/min。高转速导致高频啸叫，而且电驱动系统的动态响应频率进一步提高至2k Hz～5k Hz，该频率在人耳的敏感频率范围之内，严重影响了汽车的乘坐舒适性。电驱动系统刚柔耦合建模及动力学特性分析方法，包括电驱系统整体动力学建模、电驱动系统各部件刚柔耦合建模、电驱动系统动力学响应计算、电磁激励下的电驱动系统动态响应分析、齿轮传递误差激励下系统动力学响应分析。

针对多自由度系统的整体建模，首先需要将整个模型进行离散化。目前常用的离散化方法主要有集中参数法和有限元建模法，基于有限元原理对具有复杂构型的多自由系统进行动力学建模更加符合系统本质特性，本文借鉴有限元法原理进行电驱动系统整体动力学方程的建立。基于有限元原理的电驱系统动力学方程由相应的各零部件单元质量矩阵、刚度矩阵、阻尼矩阵构成。遵照以下原则：

(1)轴单元建模采用铁木辛柯梁单元进行建模，考虑剪切变形，忽略摩擦因素；

(2)轴单元的质量矩阵采用一致质量矩阵，考虑相邻节点的质量耦合；

(3)以节点的形式将齿轮啮合刚度的等效弹簧添加到传动轴上。电驱系统整体动力学方程如下：

Mq+Cq+Kq=f

(1)

式中，M为系统质量矩阵，C为阻尼矩，K为刚度矩阵，f为激振力矩阵。

求得各零部件单元的质量矩阵、刚度矩阵、阻尼矩阵，就可按照一定的方式组装入系统全局质量矩阵、刚度矩阵、阻尼矩阵中，进而可以利用数值计算方法进行动力学方程求解。

电驱动系统各部件刚柔耦合建模包括电机及箱体柔性有限元建模、异形轴类部件的有限元建模、齿轮啮合单元动力学建模、轴承单元的动力学建模。

将箱体的三维几何模型导入到有限元软件进行网格划分。因电驱系统箱体是不规则壳体，所以这个过程首先需要做几何清理，进而是网格划分、网格质量检查和网格处理的迭代过程，最终保证网格质量、数量要求。

图1 电驱系统箱体网格
Fig.1 Meshing of electric drive system box

设置各部分壳体的有限元模型材料，包括密度、杨氏模量、泊松比等材料属性；在输入轴、中间轴、输出轴、电机转子轴对应轴承座孔处建立凝聚节点的位置，使其与轴承外圈进行耦合。在电驱系统箱体悬置点处添加约束，及箱体模型接地等边界条件；对有限元模型进行缩聚，最终得到箱体缩聚的刚度矩阵与质量矩阵。

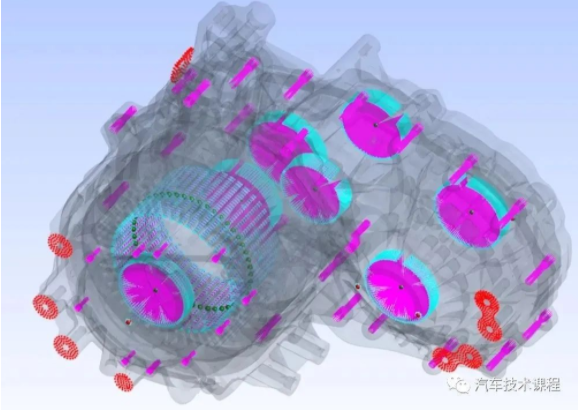
图2 电驱系统凝聚节点位置
Fig.2 Condensation node of electric drive system

与电驱动系统箱体不同之处，是差速器壳体由于是轴类零件，不需要进行接地处理，但额外需要与齿轮轮辐进行连接。

将差速器壳体的三维几何模型导入到有限元软件进行网格划分。因差速器壳体也是不规则壳体，所以这个过程首先需要做几何清理，进而是网格划分、网格质量检查和网格处理的迭代过程，最终保证网格质量、数量要求。

图3 差壳网格划分及凝聚节点位置
Fig.3 Differential meshing and node location

设置差速器壳体各部分有限元模型材料，包括密度、杨氏模量、泊松比等材料属性。在差速器两个轴承内圈连接处中心建立凝聚节点，同时在齿轮轮辐连接区域中心建立凝聚节点，以及在差速器内锥齿轮左右垫片处、上下定位销处建立凝聚节点。并分别将轴承内圈的连接区域和齿轮轮辐连接区域基于运动耦合约束连接至凝聚节点处。对有限元模型进行缩聚，最终得到差壳缩聚的刚度矩阵与质量矩阵。

对于电驱动系统减速器中的斜齿轮啮合单元，按其结构形式可划分为轮齿啮合部分及齿轮轮体部分。针对这两部分需采用不同的建模方式进行建模。

(1)针对轮辐，轮辐不是具有规则回转结构的回转体，其包含减重孔。同差速器壳体一样进行有限元建模，其中轮辐只需连接轴外圈及齿轮啮合位置的柔性节点圈。

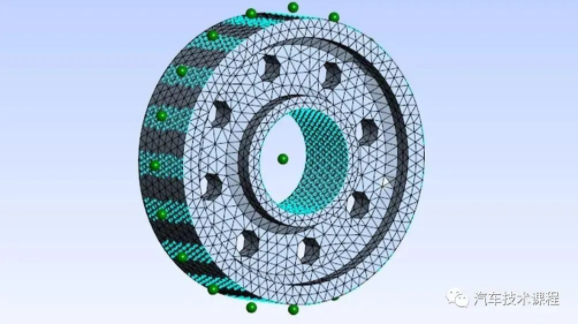
图4 轮辐网格划分及凝聚节点位置
Fig.4 Spoke meshing and node location

(2)针对斜齿轮齿的建模，采用参数化建模。其中主要分成两部分，为渐开线啮合部分、齿根圆弧部分。各部分的网格数量及大小可通过软件识别齿轮的宏观参数任意控制，同时生成这两部分的有限元网格模型。

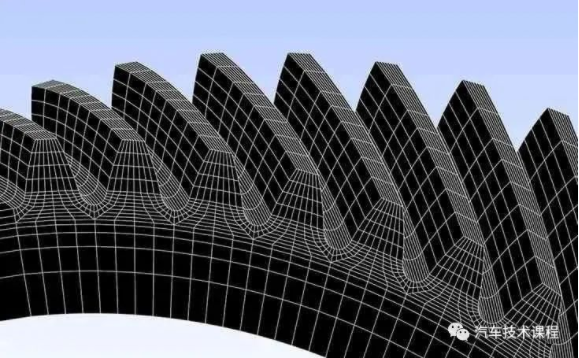
图5 斜齿轮参数化建模示意图
Fig.5 Parametric modeling of helical gear

由于轴承相比电驱动系统其他各部件质量小得多，故对轴承质量忽略不计。另轴承内圈与轴相配合，轴承外圈与壳体凝聚节点相耦合。其耦合方式有三种，分别为刚性模型、非耦合弹性支撑模型以及耦合弹性支撑模型，其中耦合弹性支撑模型最为普遍。同时考虑到电驱系统箱体柔性对轴承位移作用的影响，最终得到轴承和箱体单元的运动动力学方程。

动态啮合刚度指啮合齿轮受到单位微米大小的正弦传递误差激励而计算出的动态力，动态啮合刚度是随齿轮啮合频率ω变化而动态变化的轮齿啮合刚度。

ω=n/60×Z

(2)

D(ω)=C(ω)-1

(3)

C(ω)= C1 (ω)+C2(ω)

(4)

式中，n为转速，Z为齿数，ω为齿轮啮合频率，D(ω)为当频率是ω时的齿轮啮合线上的动态啮合刚度，C(ω)为两齿轮总柔度，C1(ω)和C2(ω)为主从齿轮在啮合线上的柔度。

齿轮副动态啮合力是指啮合齿轮副受到静态传递误差谐波激励而计算出的轮齿动态力。

Fi(ω)=D(ω)× δi

(5)

式中，Fi(ω)为齿轮传递误差第i阶谐波的动态啮合力、δi为齿轮啮合传递误差的第i阶谐波。

(K-ω2rM)φr=0

(6)

式中，ωr为第r阶固有频率，φr为第r阶固有振型，M为质量矩阵，K为刚度矩阵。上式要求特征值ωr所对应的特征向量φr是正交的，系统的质量矩阵M及刚度矩阵K同时正交的，即可得到系统的固有频率及模态振型。

由电驱动系统振动噪声的传递路径可以得出，振动噪声传至壳体之后，一方面通过壳体振动直接向空气中辐射噪声，另一方面通过电驱动系统与车辆的连接点向车辆其他部件传递振动，引起车辆其他部件的共振或者借助其他部件向外辐射噪声。同时电驱动系统与车辆的连接点一般为系统悬置点或者固定连接处，因此分析悬置点处的振动加速度可对NVH性能进行评价。分别对电机的扭矩波动的24阶、48阶谐波所引起的对电驱系统的三个悬置点位置处的振动加速度响应做分析。

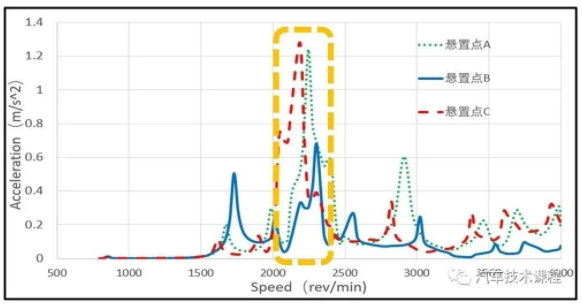
图6 转矩脉动24阶系统动力学响应
Fig.6 Dynamic response of 24 with torque ripple

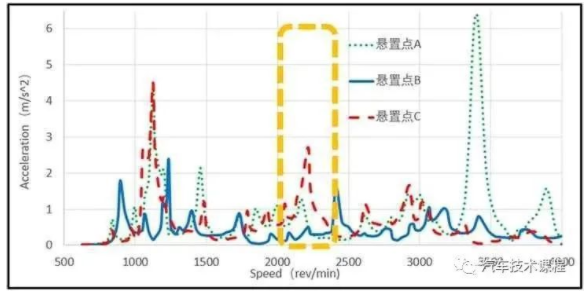
图7 转矩脉动48阶系统动力学响应
Fig.7 Dynamic response of 48 with torque ripple

(1)由图6、图7可知，电机转矩脉动24阶谐波和48阶谐波的NVH激励源作用下，悬置点A处的振动加速度均值要比另外两个悬置点B、C均值较大一些，这是，因为悬置点A处离NVH激励源较近，因此受激励源的影响较大；

(2)由图6、图7对比可知，转矩脉动48阶谐波激励下的振动加速度均值要比24阶高出一个量级，转矩脉动24阶谐波激励下最大振动加速度出现在2 200 r/min，其最大振动加速度幅值为1.285 m/s2；而在转矩脉动48阶谐波激励下最大振动加速度出现在3 750 r/min，其最大振动加速度幅值为6.234 m/s2；这是由于扭矩波动的48阶谐波力比24阶的谐波力更大；

(3)在24阶次下，在输入轴转速2 300 r/min左右时，悬置点A、B、C在898 Hz频率时出现了共振峰，其振动加速度幅值分别为1.225 m/s2、0.67 m/s2、1.285 m/s2，此共振峰峰值较大。同样在48阶次下，在输入轴转速2 300 r/min 左右时，悬置点A、B、C在898 Hz频率时出现了共振峰，其振动加速度幅值分别为1.5 m/s2、0.4 m/s2、2.85 m/s2，此处共振峰值较大，需要重点关注该频率的共振。

同电机扭矩波动相同，分别对电机的径向电磁力激励的24阶、48阶谐波所引起的对电驱系统的各个悬置点位置处的振动加速度响应做分析。

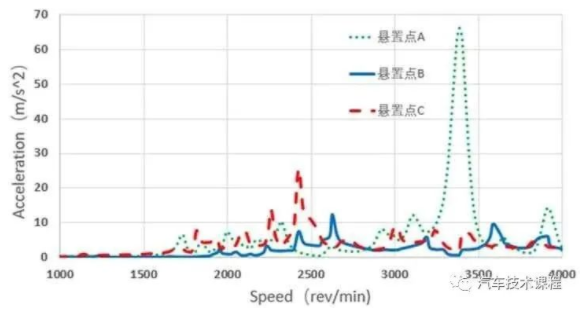
图8 径向电磁力24阶系统动力学响应
Fig.8 Dynamic response of 24 radial ele-force

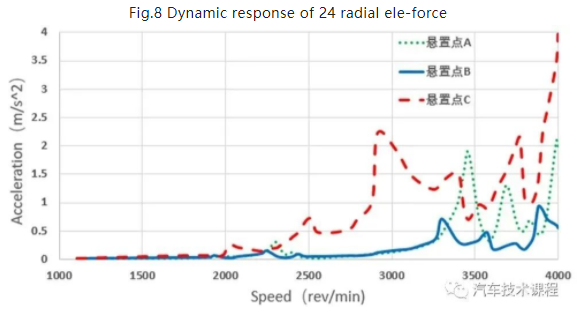
图9 径向电磁力48阶系统动力学响应
Fig.9 Dynamic response of 48 radial ele-force

(1)随着谐波阶次的增加，振动加速度幅值在0～4 000 r/min 范围内也是依次增加的，而径向电磁力24阶、48阶的谐波力幅值则是降低的，这是由于谐波阶次增加，其工作频率也在相应增加，因此其幅值也相应地更高，而在相同的工作频率下对比，则其振动加速度幅值与谐波力幅值的表现一致。

(2)悬置点A、C在转速为3 690 r/min出现了共振峰，其24阶振动加速度峰值分别为1.35 m/s2、2.12 m/s2，其共振的固有频率可能为2 950 Hz；悬置点B、C在转速为2 450 r/min 出现了共振峰，其48阶振动加速度峰值分别为7.05 m/s2、26.0 m/s2，其共振的固有频率可能为1 950 Hz；悬置点A在转速为3 460 r/min 时出现了一个较大的共振峰，其48阶振动加速度幅值为68 m/s2，其共振的固有频率可能为2 800 Hz，需重点关注这几个频率的共振。

分别对减速器齿轮啮合的一、二级两对齿轮副的传递误差进行傅里叶变换，分别获得起传递误差各阶谐波，由于传递误差的二阶及以上谐波幅值较小，可忽略不计。故只考虑将一二级齿轮的一阶谐波作为NVH的激励源。分析一、二级齿轮副的激励源所引起的对电驱系统的各个悬置点位置处的振动加速度响应。

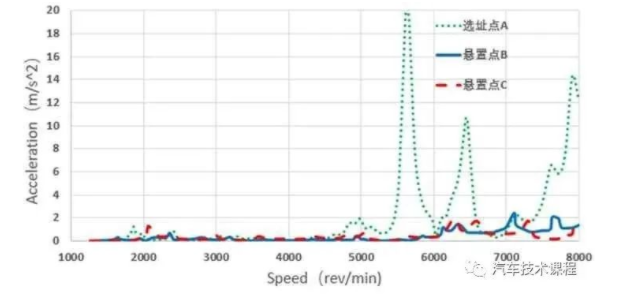
图10 一级齿轮TE的动力学响应
Fig.10 Dynamic response of 1st gear TE

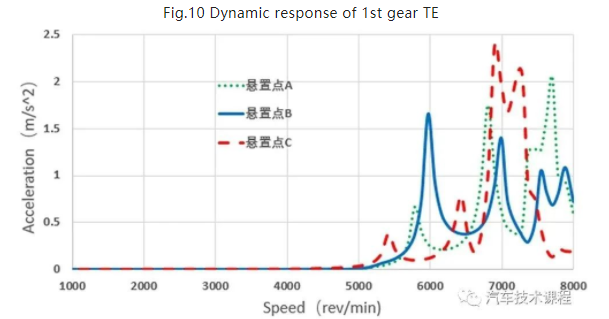
图11 二级齿轮TE的动力学响应
Fig.11 Dynamic response of 2nd gear TE

(1)在输入轴低转速的情况下，系统振动及速度幅值较低，随转速增加，振动加速度幅值总体呈上升趋势；

(2)传递误差越小，一阶谐波幅值越小，振动加速度幅值越小，越有利于NVH;

(3)将一、二级齿轮副啮合引起的振动加速度幅值同电机扭矩波动、径向电磁力激励下的振动加速度幅值进行比较，可得出二者对系统NVH的贡献量，振动加速度幅值越大，贡献量越大；

(4)在二级齿轮副啮合阶次下，在转速为6 950 r/min附近时，三个悬置点出现了第一次共振峰，三个悬置点处的加速度峰值分别为1.76 m/s2、1.41 m/s2、2.39 m/s2，在此转速附近，具有2 750 Hz与3 290 Hz的固有频率；这种情况是激发起系统的某一固有频率引起的，需重点关注该固有频率的共振情况。

针对电驱动系统NVH分析及优化中存在的高转速、多源激励以及整体强耦合性等难题，基于有限元及动力学建模方法，搭建了电驱动整体刚柔耦合动力学模型。本文分别对驱动电机及箱体的有限元建模以及齿轮传动系统动力学建模两大方面进行了详细建模。针对驱动电机建模部分，采用有限元模型缩聚的方式进行了电驱动箱体与电机定子的建模工作，同时还有对电磁力的施加处理方法。针对齿轮传动系统，建立了弹性轴段、斜齿轮啮合单元、差速器壳体单元以及轴承单元的动力学模型。基于以上建模流程，形成了电驱动系统整体刚柔耦合建模方法。接下来给出了电驱动系统动力学响应的计算方法。最后，针对驱动电机径向力、转矩脉动以及齿轮副传递误差等 NVH 激励源作用下的系统动态响应进行了对比分析。